Jordan curve illustrations: a triangular example
There is a Jordan curve such that every piecewise-linear path from the inside to the outside intersects the curve infinitely many times. I sketch the construction of such a curve here.
Triangles instead
Last time I described the very simple class of rectagons. I also gave a way to represent these curves different as a sequence of movement tokens. There were three movement tokens: left, right, and straight. For simplicity’s sake, it would be most convenient only to have two movement tokens. (Such curves would be arguably more “digital” than the previous curves.) I was unable to get this to work for a grid of squares. Parity problems got in the way. So I ditched the squares and used equilateral triangles instead.
For triangles, there is no straight movement token. Only Port and Starboard movements are possible. The question is what the local picture of a wiggling of the curve should be. Happily the picture will look the same in all triangles.
Note that we don’t want an isotopy of the curve fixing the boundary of the triangle. No such triangle-local isotopy can give us the sort of Jordan curve we want. The triangle edges would end up being piecewise-linear paths from the inside to the outside. Instead we just show the intersection of the triangle with the wiggled curve.
Hex curves and turns
More formally, suppose \(T\) is an equilateral triangle. Let \(C\) be its centroid. A bend in \(T\) is the union of two feet from \(C\) perpendicular to two sides of \(T.\) There are three bends in every triangle. Suppose \(PP\) is a 6-regular triangulation of the plane by equilateral triangles. A hex curve subordinate to \(PP\) is a PL curve that is the union of bends in triangles of \(PP.\)
An oriented bend is a turn. Every triangle has six turns possible in it. The turns have two orbits under the three rotational symmetries of \(T.\) One orbit consists of port turns; the other consists of starboard turns. Up to orientation-preserving isometry, a oriented hex curve is determined by its corresponding sequence of port and starboard symbols “P” and “S,” which we will call its course.
Our aim is to give a function \(f\) from hex curves to hex curves, such that
- \(f(\gamma)\) is isotopic to \(\gamma;\)
- for all hex loops \(\gamma,\) \(\gamma_\infty = \lim_{n\to \infty} f^{\circ n}(\gamma)\) is a Jordan curve; and
- for all hex loops \(\gamma,\) every piecewise-linear path between the inside and outside of \(\gamma_\infty\) intersects \(\gamma_\infty\) in infinitely many points.
The turn-local picture of a wiggling
As with wiggling the rectagons, a wiggled hex curve will no longer be subordinate to its original triangulation. Instead, the new curve is subordinate to a finer triangulation. For our choice of \(f,\) the new triangulation has eighty-one triangles per previous triangle, dividing the sides of the triangles into nine equal pieces. Equivalently, the new triangulation is the old triangulation scaled down by a factor of nine by homothety at a vertex.
The local picture \(\gamma' \cap T\) of the wiggling is the same for both orientations of a bend. However, it is most convenient to give the local picture via its courses. This requires orientations. So I will give the courses (and starting triangles) for the components of the local picture after wiggling a port turn, and after wiggling a starboard turn.
Suppose we want to wiggle a port turn. Let \(A\) be the side at which the turn begins, and \(F\) the side at which it ends. Then the other side \(S\) of the triangle is starboard of the (port) turn, and the vertex is port of the turn. Nine new triangles are incident to \(A.\) Order them \(T_0^A,\ldots,T_8^A\) from port to starboard. Likewise, nine new triangles are incident to \(F.\) Order them \(T_0^F+,\ldots,T_8^F\) from port to starboard. The components’ boundary points lie in the triangles \(T_3^{A,F},T_4^{A,F},T_5^{A,F}.\) To wit, the (three) components of \(f(\gamma) \cap T\) are as follows:
- \(M\) starts from \(T_3^A\) with course \(PSPSSSSPSPS,\) and thus ends at \(T_4^A;\)
- \(Y\) starts from \(T_5^A\) with course \(PSPSPSPPSPS,\) and thus ends at \(T_3^F;\) and finally,
- \(C\) starts from \(T_4^F\) with course \(PSPSSPSPSPSPPPPSPSPSPSPPSPS,\) and thus ends at \(T_5^F.\)
Here is what that looks like in the triangle of a bend:
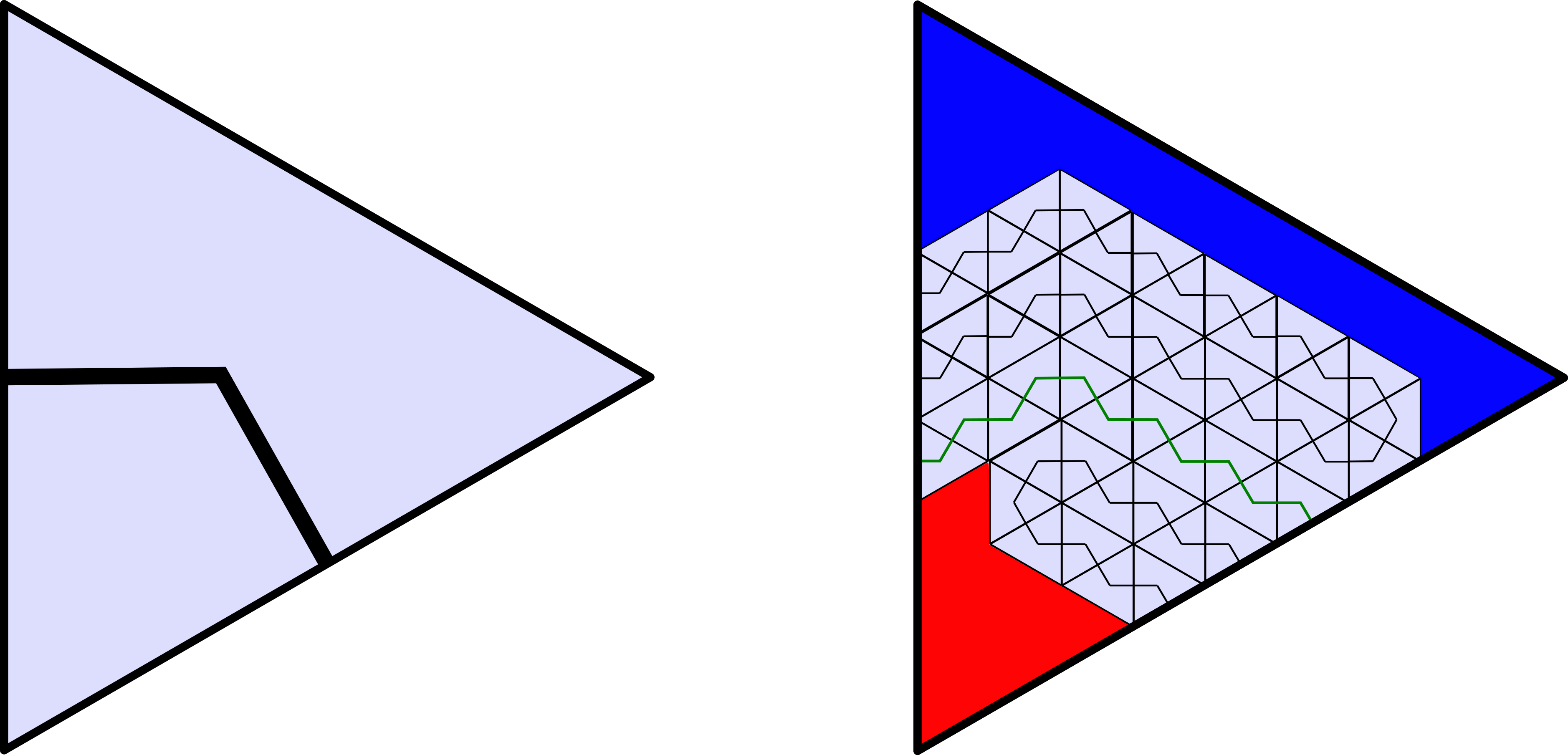
Curiously the courses all start and end with the sequence \(PSPS.\)